독후감

복잡계 개론

지나가는물리학부생 2023. 4. 25. 23:31
반응형

제목 : 복잡계 개론

저자 : 윤영수, 채승병

ISBN : 9788976332813(8976332814)

 

독서기간 : 2023-02-21 ~ 2023-02-25

 

1장 : 복잡한 세상으로의 초대

    1. 다이내믹한 현상에 어떻게 접근할 것인가?

세상은 다이내믹(dynamic)하다. dynamics는 다양한 변화를 기술하기 위한 이론체계이다.

하지만, 현실 세계는 dynamics로 이해하기는 힘들다.

심지어 점점 '복잡(complex)'해지고 있다!

 

black friday의 대폭락은 왜 갑자기 발생했으며, 또 놀랄 만큼 신속하게 진정되었는가?

Y2K의 소동은 단순한 소동인가? 아니면 성공적인 재난 방지의 사례인가?

 

사회 경제 분야의 현상들이 갈수록 복잡해져 점점 예측이 어려워진다.

    -> 현상에 관여하는 개체의 종류와 수가 많으며, 각 개체들 각각의 행동을 지배하는 법칙을 잘 알지 못한다.

 

그러면, 복잡한 현상에 어떻게 접근할 것인가?

최대한 단순화된 설정부터 탐구하자.

    -> 모든 개체들이 똑같은 종류라고 가정, 운동이 무작위적(random)이라고 가정

    2. 복잡한 현상을 가로지르는 거시적 질서

복잡계에서 발생하는 대표적인 질서현상으로는 거듭제곱법칙(power law)이 있을 것이다.

예시) 지진의 규모에 따른 발생 빈도, 면화의 시장 가격변동 분포, 영어단어 빈도 분포 등

 

이러한 거듭제곱법칙은 사회, 경제계 뿐만 아니라 정보통신, 생명과학에 이르기까지 많은 사례를 망라한다!

    3. 복잡계와 복잡성이란 무엇인가?

복잡계의 핵심적인 특징 : 창발

 복잡계는 수많은 구성요소들로 이루어져 있고, 다양한 상호작용을 주고받는다.

이에 따라, 구성요소들을 따로따로 놓고 봤을 때의 특성과는 다른 거시적인 새로운 현상과 질서가 나타난다.

이를 '창발(emergence)'이라고 한다. 이로 인해 나타나는 질서적인 현상을 '창발현상(emergent behavior)'이라고 한다.

* 거듭제곱법칙으로 드러나는 통계적인 질서도 전형적인 창발현상이다.

 

복잡계의 정의와 특징

복잡계의 개념과 이론은 통일된 정의가 없다.

일반적으로 받아들여지고 있는 복잡계로서 갖춰야 할 특징을 정리하면 아래 다섯 가지로 나눠볼 수 있다.

    1) 복잡계는 상호작용 하는 많은 구성요소를 가지고 있다.

        -> 시스템 전체를 이해하는 데 개별요소들 이상으로 요소들의 연관관계와 상호작용을 이해하는 것이 중요

    2) 복잡계 구성요소들의 상호작용은 흔히 비선형적(nonlinear)이다.

        -> 극히 작은 요동도 구성요소들 사이를 전파해 나가면서 증폭되어 커다란 영향을 미칠 수 있다.

    3) 복잡계 구성요소들의 상호작용은 흔히 되먹임 고리(feedback loop)를 형성한다.

        -> 구성요소들 사이의 상호작용은 한쪽 방향으로만 이뤄지지 않고 다양한 경로를 거침

        -> 복잡계에서는 되먹임 고리를 통해 전혀 예기치 않았던 방향의 결과가 종종 관찰된다.

    4) 복잡계는 열린 시스템(open system)이며 그 경계가 불분명하다.

        -> 열린 시스템이라는 것은 외부환경과 차단되어 있지 않고 끊임없이 영향을 주고받는다는 것이다.

    5) 복잡계의 구성요소는 또 다른 복잡계이며 종종 끊임없이 적응해 나간다.

        -> 시장을 구성하는 기업, 다시 그 기업을 구성하는 부서, 부서를 구성하는 인간은 모두 하나의 복잡계이다.

        -> 적응하는 구성요소들로 이루어진 복잡계를 특히 복잡 적응계(Complex Adaptive System : CAS)라고 한다.

 

'더욱 복잡하다(more complex)'는 것, 또는 '높은 복잡성(higher complexity)을 갖고 있다'는 것은

'그 대상(또는 현상을 기술하는 데 더 많은 정보가 필요하다'는 의미이다.

구체적으로 복잡성의 정도를 재는 척도를 복잡도(complexity measure)라고 한다.

 

똑같은 대상에 대해 이야기하더라도 이를 바라보는 축척(scale)에 따라 복잡성의 정도가 달라진다.

2장 : 복잡계 이론의 배경

    1. 단순한 바탕을 찾아서 : 환원주의 과학방법론의 정립

'오컴의 면도날'은 인과적 결정론(casual determinism)과 방법론적 환원주의(methodological reductionism)의 중요한 바탕

'더 이상 간단해질 수 없는 본질의 밑바닥을 찾자!'

    2. 복잡한 전체를 향하여 : 전일주의 과학방법론의 등장

결정론은 '열현상'에서 문제가 제기되었다.

 

열현상은 분자들의 운동만으로 충분히 설명이 가능하지만, 분자가 너무 많다 + 분자 사이의 상호작용도 알아야 한다

    = 기체분자의 동역학을 통계적으로 다루기 시작함

 

따라서, 기체분자의 동역학을 통계적으로 다루기 시작했다!

 

열역학에서는 시간의 변화가 한 방향으로만 진행된다 (엔트로피가 증가하는 방향)...!

엔트로피는 이 책에서 그렇게 중요하지 않은것 같아 생략하겠다.

 

통계역학의 방법론은 비가역성과 시간의 화살 문제를 통해, 개개 입자의 차원에서는 드러나지 않는 특징이 수많은 입자들이 얽히면서 거시적으로 나타날 수 있음을 알게 되었다.

 

생물 외부환경의 영향이 생존과 변이에 핵심적인 영향을 줌.

    -> 생물을 물리법칙이 지배하는 기계로 파악하는 관점만으로는 진화에 접근하기 힘듦.

 

생태계는 왜 다양한 모습을 가지며, 어떻게 살아가기에 적합한 자기 조절 능력을 가지게 되었는가?

 

진화적 게임 이론

게임 이론 + 진화론 = 진화적 게임 이론

대표적 실험 예시 : 반복적 죄수의 딜레마(Iterated Prisoner's Dilemma : IPD)

    3. 현대 복잡계 이론의 문턱

시스템 이론

열역학 제2법칙에서 다루는 닫힌 시스템은, 아무런 특이점이 없는 열평형상태가 확정.

그러나, 적응하고 진화하며 분화되는 생명현상, 즉 복잡성이 증가하는 현상은 없다!

 

열린 시스템(open system)을 받아들이자!

    =시스템 이론(systems theory, systemics)

시스템 : 상호작용 하는 개체 또는 개체군으로 이루어진 총체

사이버네틱스(cybernetics), 파국 이론(catastrophe theory),

혼돈 이론(chaos theory), 복잡계 이론(complex systems theory)

 

cybernetics : 살아 있는 생물체나 복잡한 기계에서 보이는 자가규제 시스템(self-regulating system)에 대해 연구하는 분야.

                     수시로 변화하는 조건들을 극복하며 예정된 목표를 향해 나아가도록 하는 것이 중요한 목적임.

                     감각기관들로부터 얻어지는 정보를 처리, 무의식적으로 반응하는 되먹임

 

catastrophe theory : 단절적인 변화에 대한 수학적인 설명의 하나.

                                급격한 변화를 어떠한 안정상태들 사이의 급격한 전이로 바라보고, 이를 수학적으로 뒷받침하는 이론.

                                항상 안정된 평형상태를 따라 나아간다는 점에서 한계가 있음.

 

혼돈 이론이 등장하면서 평형상태로 가지 않고도 기이한 끌개를 형성하거나 발산해버리는 등 다양한 다이내믹스를 가지는 상황이 있음을 알게 됨.

3장 : 복잡계 이론

복잡계 이론은 다양한 분야에서 복잡성과 창발에 대한 인식이 자리를 잡음

    -> 이제 그들 사이의 상호작용이 어떻게 창발현상을 만들어내는지를 알아야 함

    1. 복잡계의 이론체계

복잡계는 수많은 구성요소들로 이루어져 있고, 상호작용을 한다.  -> 비선형적임!

비선형적이라는 것은, 시스템이 작은 변동에도 민감하기 반응할 수 있다는 것을 의미함  = 혼돈(chaos)

 

여러 비선형 상호작용이 밎어내는 현상에는 나름대로 반복되는 질서가 있음.

커다란 축적에서 발견되는 구조를 자세히 들여다보면 작은 축적에서도 똑같은 구조가 반복됨

    -> 자기유사성(self-similarity), 이런 도형을 프랙탈(fractal)이라고 함.

 

축척의 변화에 따라 관찰되는 고도의 조직은 어떻게 만들어지는가?

ex) 국가, 기업을 비롯한 인간사회의 여러 조직과 업무는 어떻게 저절로 만들어 졌는가?

복잡계는 열린 시스템임 -> 외부로부터 에너지가 드나들 수 있음 -> 개별요소들의 상호작용 -> 새로운 계층의 조직을 만듦

이러한 창발적인 질서를 만들어가는 과정이 자기조직화(self-organization)임.

 

임계현상 : 특정한 임계점(critical point)을 전후하여, 시스템의 조건이 조금씩 변함에 따라 거시적인 상태가 아주 크게 변함

임계점에 멀리 떨어져 있을 때 - 무질서한 상태

    => 임계점에 접근 - 구성요소들이 규칙을 갖고 모이면서 새로운 질서를 만들어냄

 

자기조직화된 임계성(Self-Organized Criticality : SOC) : 외부에서 시스템의 조건을 인위적으로 조절해주지 않아도 내부의 자기조절 과정을 통해 이러한 임계상태로 스스로 전이해가는 것

많은 복잡계에서 자기조직화된 임계성이 보임.

    2. 혼돈과 기이한 끌개

혼돈의 본질 : 초기조건에의 민감성(sensitivity to the initial condition), 나비효과(butterfly effect)

 

기이한 끌개

끌개(attractor) : 주어진 조건 하에서 물체의 운동이 귀결되는 상태

                         일정한 시간이 지난 뒤에 그 궤적이 끌려가는 점 또는 그러한 점들의 집합

단진자 운동을 예시를 들어보자.

마찰이 있을 경우, 진자의 진폭이 조금씩 줄어들다가 원점에 멈추게 될 것이다.

    -> 원점이 끌개! => 점 끌개(point attractor)

마찰이 없을 경우, 계속 진동하게 될 것이다. 속도, 거리의 위상공간이 있을 경우 계속 타원을 그릴 것이다.

    -> 타원이 끌개! => 한계순환 끌개(limit cycle attractor)

이 외에도 여러 종류의 끌개가 있다.

 

아래 그림은 로렌츠 방정식의 해가 그리는 궤적이다.

이 그림을 보면 궤적이 어떤 점에 수렴하는 것도 아니고, 모양이 일정한 타원이나 토러스에 수렴하지도 않는다.

그렇다고, 아예 불규칙하지도 않다.

나름의 기이한 구조를 그린다.

이를 기이한 끌개(strange attractor)라고 한다.

이런 기이한 끌개가 나타나는 운동은 혼동운동의 특징을 지닌다.

 

주기배가

로지스틱 사상(logistic map)은 간단한 2차 다항식으로 주어지는 이산 시간 동역학계이다.

$x_{n+1}=\gamma x_n(1-x_n)$

$\gamma$를 증가시키는 것은 비선형성을 증가시키는 것을 의미

$\gamma$가 낮을 때는 멸종하며, 커짐에 따라 균형을 유지한다. 어느 시점으로 커졌을 때 주기배가가 일어난다.

$\gamma$가 커짐에 따라 주기배가의 속도도 더 빨라지다가 어느순간 혼동상태를 보임.

$\gamma$에 따른 안정된 상태의 개체 수

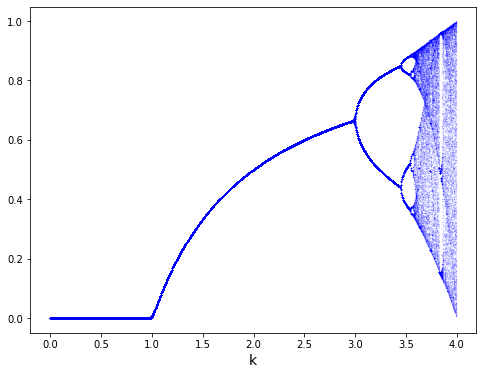
위 그래프에서 k는 $\gamma$이다.

 

$\gamma$가 약 1보다 작은 영역에서는 멸종

$\gamma$가 약 1~3 의 영역에서는 정상상태

$\gamma$가 약 3~3.5 의 영역에서는 정상상태이지만 두 개의 값을 진동하는 것을 볼 수 있다.

$\gamma$가 약 3.5보다 큰 영역에서는 엄청난 가능성이 있어 혼돈 영역이라고 할 수 있다.

 

이때, 주기배가를 일으키는 매개변수값이 일정한 등비수열의 형태를 띄고 있음을 발견한다!

    -> 이를 파이겐바움의 보편상수라고 부른다.

        -> 주기배가가 일어나는 분기점(bifurcation point)의 거리 사이의 비율에서 나타나는 보편상수

    3. 프랙탈과 자기유사성

프랙탈

프랙탈 : 일부 작은 조각이 전체와 비슷한 기하학적 형태를 말한다.

    -> 자기유사성과 프랙탈 차원(fractal dimension)의 개념으로 구성되어 있다.

            자기유사성 : 어떤 일부를 확대해 보더라도 전체 모습과 본질적으로 닮았다는 것.

                        -> 똑같다는 것이 아니라, 통계적인 특성이 같아도 자기유사성이 있다고 할 수 있다.

            프랙탈 차원 : 공간에 패턴을 얼마나 조밀하게 채우는지 나타내는 비율

 

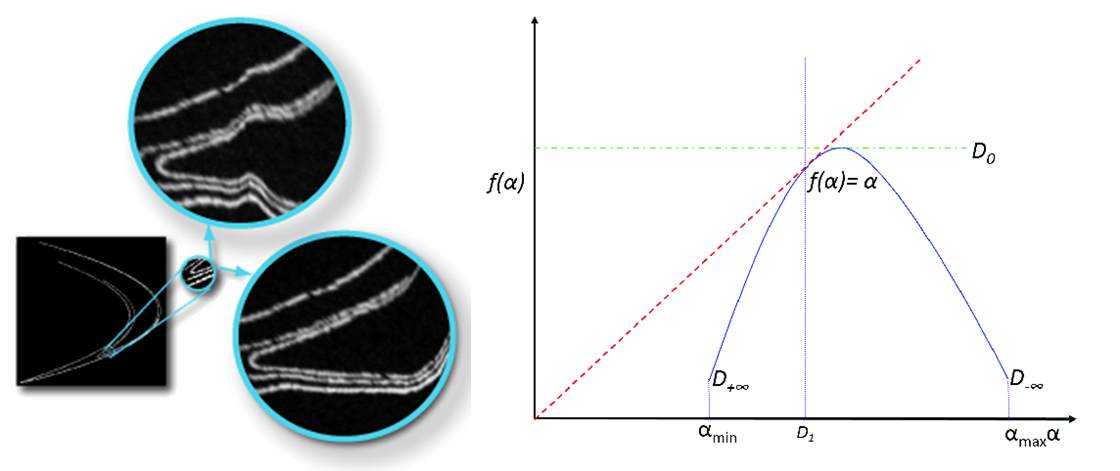
왼쪽 그림 : 다중 프랙탈 예시, 오른쪽 그림 : 특이성 스펙트럼(singularity spectrum)의 예시

측정하는 부분마다 그 프랙탈 차원이 다른 구조가 섞여 있는 프랙탈을 다중 프랙탈(multifractal)이라고 한다.

 

그러면. 어떻게 분석해야 할까?

특이점에서의 프랙탈 차원을 계산하고 이를 그림으로 그리면 될 것이다!

자세한건 직접 찾아보길 바란다. 그냥 그런게 있다라고 이해하자.

 

단일 프랙탈이라면 프랙탈 차원이 하나밖에 없으므로, 특이성 스펙트럼은 하나의 점으로 표시된다.

다중 프랙탈이라면 다양한 $\alpha$에 따라 퍼진 곡선의 형태로 스펙트럼이 얻어진다.

    -> 곡선의 너비가 넓을수록 다양한 프랙탈 차원을 가진다는 의미

        -> 다양한 복잡성을 가지고 있다고 해석 가능!

 

프랙탈과 자기유사성에 관한 자세한 설명은 아래 링크에서 보는 것을 추천한다.

https://horizon.kias.re.kr/12112/

    4. 스스로 만들어지는 질서, 자기조직화

앞에서 자기조직화가 뭔지는 설명 해두었다...!

베나르 대류(베나르 세포)

자기조직화의 고전적인 예시이다.

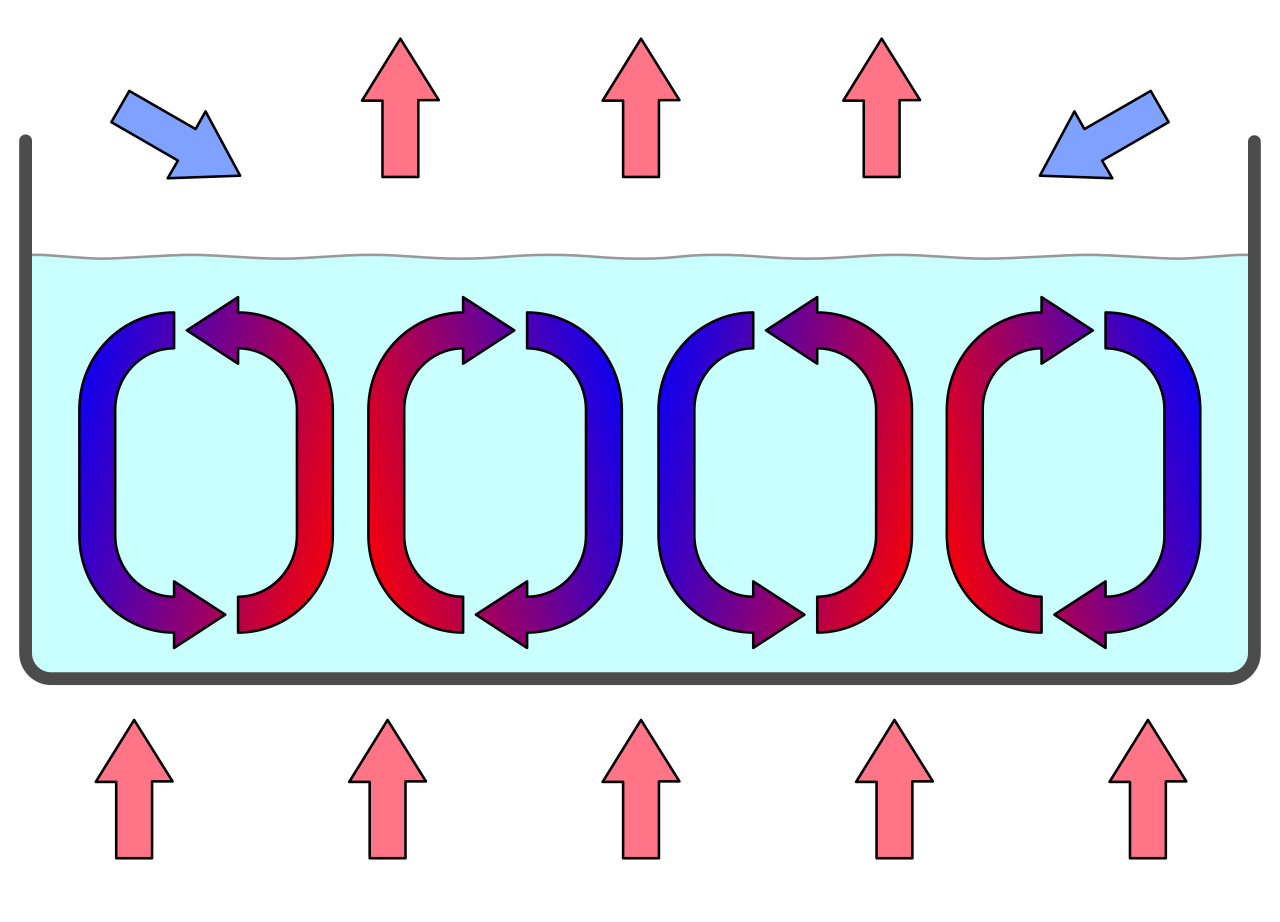
    1 단계 : 역전층(안정한 전도) - 따뜻함

    2 단계 : 혼돈적 흐름(불규칙적 대류) - 뜨거움

    3 단계 : 베나르 세포(규칙적 대류) - 매우 뜨거움

왼쪽 그림은 3 단계의 예시이다.

 

시스템이 평형상태에서 아주 멀어지면 분기현상이 일어나면서 또 다른 형태의 질서가 만들어짐!

비평형 상태가 무질서만을 만들어내는 것이 아니라, 새로운 질서의 근원!

소산구조(dissipative structure) : 이때 나타나는 복잡하지만 거시적인 안정적 질서구조

 

이 외에도, 벨루소프-자보틴스키 실험, 하켄의 시너제틱스 등의 자기조직화의 대표적인 예시가 있다.

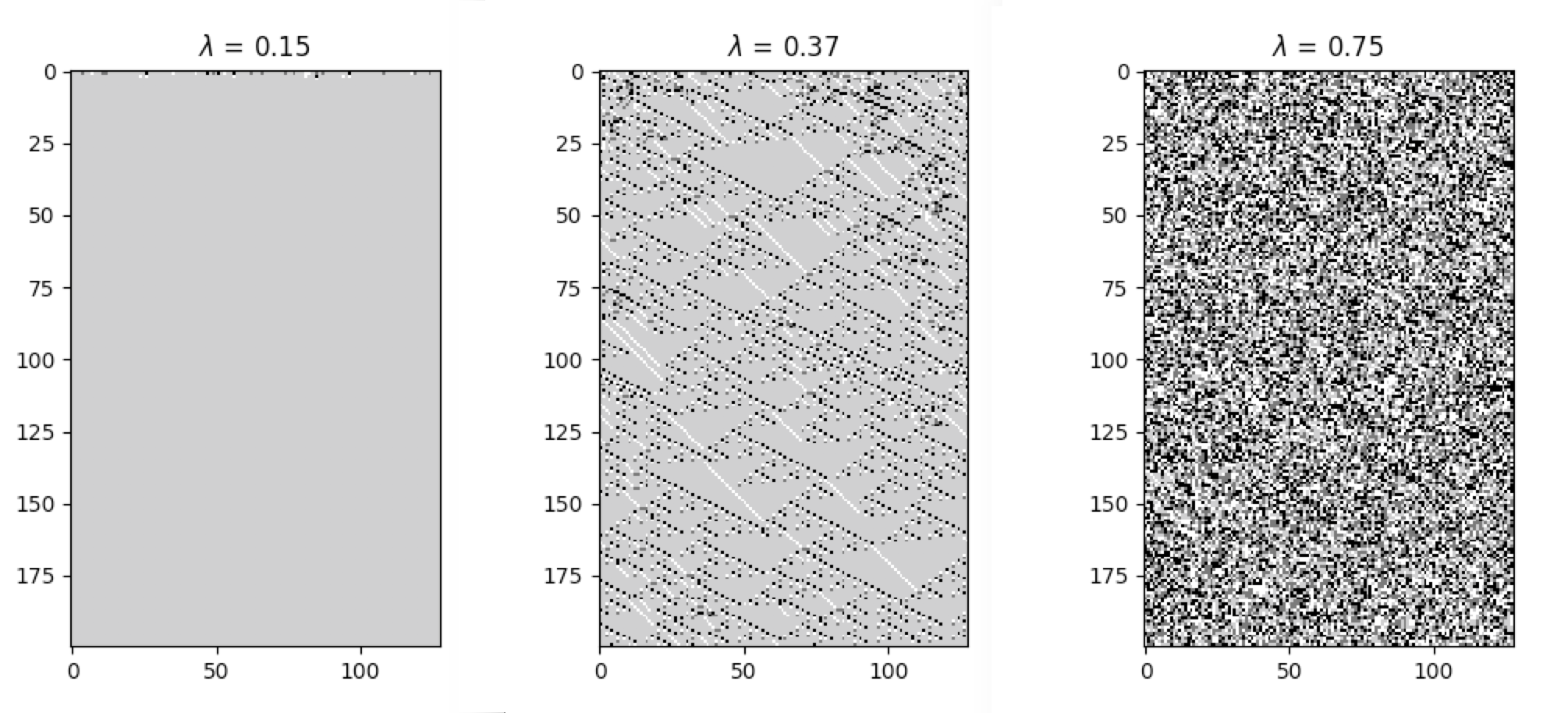
자기조직화가 흥미롭다면, 'edge of chaos'를 구글링해서 찾아보기를 추천한다.

그리고, 왼쪽 그림은 파이썬의 라이브러리를 이용하여 그린 세포자동자 시뮬레이션 결과이다.

https://github.com/lantunes/cellpylib

 

물론, 내가 그린건 아니다. 재미있어 보이기는 하지만, 그냥 읽기에 재미있을 뿐. 연구해보고 싶은건 아니라서...

 

진화론

다윈의 진화론이 나온 이래 생명체의 진화는 무작위적 돌연변이, 교배를 통한 교차 에 이어지는 자연선택에 의해 이뤄진다고 간주되었다.

1930년대에 라이트(S.Wright)가 고안한 적합도 지형(fitness landscape)을 이용하면 쉽게 확인할 수 있다.

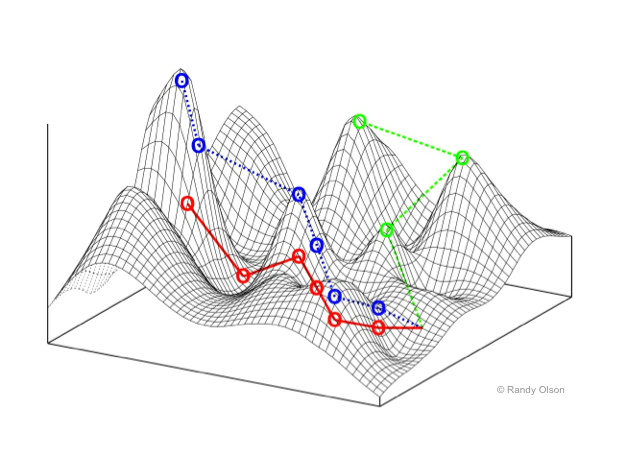
적합도 지형은 주어진 환경에서 표현형에 따른 적합도의 그래프이다. 매우 많은 표현형이 있으므로, 당연하게도 다차원 그래프이다.

왼쪽 그래프는 2차원의 경우로 예시를 들어본 것이다.

x, y축이 각각 표현형이고 z축이 적합도의 정도라고 생각하면 된다.(높으면 좋다)

적합도가 높다는 것은 그만큼 환경에 적합한 형질을 갖는다는 의미

다윈의 진화는 끊임없이 표현형을 변화시켜가며 적합도 지형의 꼭대기를 향해 나아가는 과정으로 이해할 수 있다

 

만약, 환경이 크게 변해서 적합도 지형이 무너진다면?

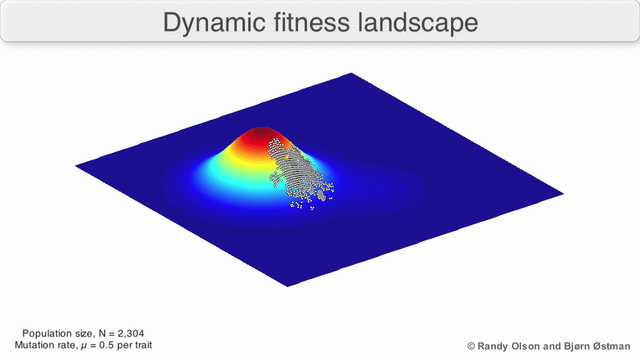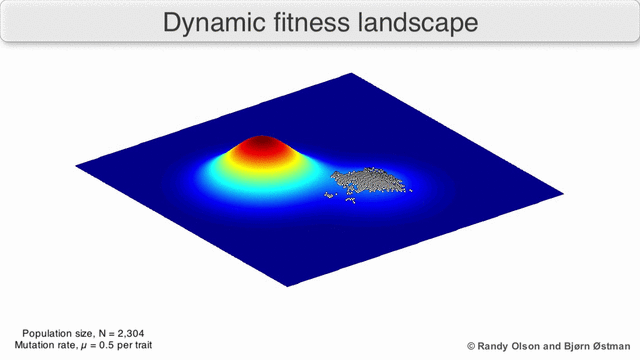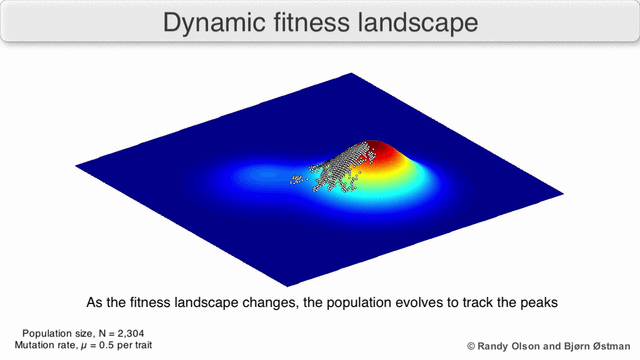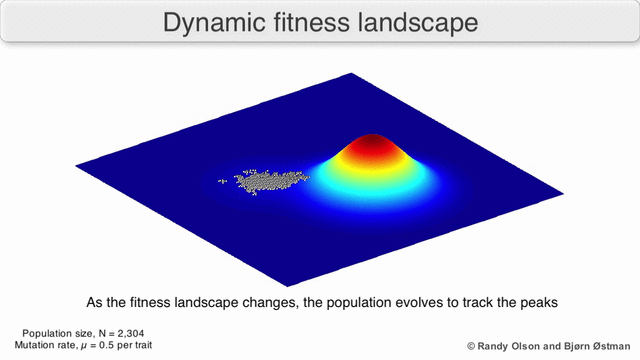
왼쪽 gif 처럼 적합도 지형 자체가 변하는 경우를 이른다.

이렇게 급속히 바뀌면 서둘러 다른 표현형으로 진화해야 한다.

만약, 유전자 네트워크의 다이내믹스가 지나치게 안정적이라면, 환경 변화에 대한 적응을 시도해보지 못하고 멸종될 것이다.

물론, 지나치게 혼돈된 상황인 경우라도 일부 적응을 시도하더라도 변화의 방향을 제대로 잡지 못하고 멸종할 것이다.

따라서 '혼돈의 가장자리(edge of chaos)'에서 예기치 않은 변화에 적응할 준비를 하고 있어야 한다!

혼돈의 가장자리에 있지 않으면, 변화 자체가 불가능하거나 매우 미미한 변화만 할 수 있으므로 그대로 도태될 위험이 크다.

    5. 자기조직화된 임계현상

임계점(critical point) : 시스템의 구성요소들을 서로 다른 방향으로 이끌고 가려는 요인이 팽팽하게 맞서 불안한 균형을 이루고 있는 지점

임계현상(critical phenomena) : 임계점 부근에서 이 균형이 깨질 때 시스템에 일어나는 거시적인 현상

 

시스템이 임계점과 멀리 떨어져 있으면 -> 시스템 요소들 사이의 상호작용이 작다.

이 상태에서는 시스템 일부에 아무리 섭동을 가해도 그 영향이 크게 확산되지 않는다.

임계점에 접근하면? -> 시스템 요소들 사이의 상호작용이 긴밀해짐 -> 영향이 미치는 범위가 급격히 거듭제곱법칙을 따르며 증가함 -> 이때 지수를 임계지수(critical exponent)라고 함!

 

그렇다면? -> 거듭제곱법칙을 나타내는 현상들 중에 상당수가 임계현상이지 않을까?

흥미로운 것은 이때의 임계지수가 여러 임계현상에 걸쳐 몇 종류의 값으로 귀결된다!

이를 보편성(universality)이라고 하며, 같은 임계지수를 가지는 현상은 같은 보편성 부류(universality class)에 속해있다고 한다.

 

비평형 상태의 여러 복잡계는 스스로 임계점을 찾아 접근해가는 자발적인 메커니즘을 가지고 있다.

따라서 이러한 복잡계에서는 대략적인 기본조건만 충족되어도 임계현상이 일어난다.

    -> 혼돈의 가장자리에 위치하면 임계점 가까이로 시스템이 자기조직화됨! = 자기조직화된 임계성

자동으로 임계점 가까이로 시스템이 자기조직화 -> 자동으로 '툭' 쳐도 바로 무너지는 사태가 나올수도!

    6. 복잡적응계

복잡적응계(CAS, Complex Adaptive System)

    -> 많은 구성요소를 가지고 이들이 상호작용 한다는 의미에서 '복잡'

    -> 각 구성요소들이 경험을 통해 학습하고 변화한다는 의미에서 '적응적'

가장 기본적인 구성단위인 행위자, 행위자들이 모인 메타 행위자들로 구성되며, 개별 행위자들은 이들 상호간의 자극-반응 규칙에 따라 행동한다.

지정된 행위자에 가능한 자극과 허용된 반응의 범위를 정하면 행위자가 가질수 있는 규칙의 종류 결정

    -> 행위자는 이 규칙의 범위 내에서 서로 적응하는 개체임

    -> 규칙들이 상호작용하여 학습 + 적응이 발생

    -> 행위자끼리 모여서 높은 수준의 행위자로 작용 : 메타 행위자(meta-agent)

    -> 메타 행위자끼리 모여서 새로운 메타 행위자를 형성할 수도.

 

홀랜드 : 다원행위자 시스템에 기반하여 복잡적응계에 네 가지 속성 + 세 가지 메커니즘 제시

    네 가지 속성 : 집합성(aggregation), 비선형성(nonlinearity), 흐름(flow), 다양성(diversity)

    세 가지 메커니즘 : 꼬리표 달기(tagging), 내부 모형(internal models), 구성 단위(building blocks)

 

네 가지 속성

  1. 집합성 : 같은 범주에 속한 것들을 동등하게 취급하는 집단화를 의미한다.

단순한 행위자들이 어떻게 복잡한 대규모 행동을 창발하는 가 하는 문제의 열쇠를 제공한다.

메타 행위자들 사이의 상호작용은 집단화 속성에 의해 가장 잘 표현됨!

  2. 비선형성

비선형 상호작용은 거의 언제나 합산이나 평균에 의해 예측하는 것보다 훨씬 복잡한 집합적 행동을 나타낸다.

<비선형성에 대한 내용은 위에서 많이 했다...!>

  3. 흐름

유체의 움직임에서 더 확장된 개념임.

노드(행위자)와 링크(상호작용1)로 이루어진 네트워크 속에서 자원(상호작용2)의 흐름.

시간에 따라 변화, 시간에 따른 적응의 변화와 경험의 축적을 반영.

승수효과, 재순환 효과 등의 성질을 가짐.

    -> 승수효과 : 자원이 노드와 노드를 옮겨다니며 연쇄적으로 가치를 만든다는 것

    -> 재순환 효과 : 여러 차례 순환

복잡적응계의 단절적 변화는 승수효과와 재순환효과에 의해서 만들어질 수 있음.

  4. 다양성

말 그대로, 자연에서 종의 다양성이라고 생각해도 될 것 같다.

'복잡적응계에서 행위자를 하나 없애면 계가 순차적으로 적응하여 새로운 행위자가 그 역할을 대신하는데, 새로운 행위자는 제거된 행위자와 같은 생태적 지위를 차지하고 그 행위자가 하던 상호작용을 떠맡는다.'

책에서 그대로 가져온 문장이다. 어디에선가 자주 나오는 그런 문장인 느낌...?

복잡적응계의 다양성은 적응의 산물이며, 적응의 패턴도 진화한다.

새로운 적응은 더 많은 상호작용과 새로운 생태적 지위를 만들어내는 것이다.

이러한 복잡적응계의 다양성과 상호작용의효과로 인해 질서체계, 즉 항상성이 유지되는 것이다.

세 가지 메커니즘

  1. 꼬리표 달기

복잡적응계의 집단화 결과

집단의 경계를 정의하는 데 널리 사용되는 메커니즘

계층적 조직화를 뒤에서 조절하는 메커니즘

행위자는 다른 행위자를 '꼬리표' 가지고 구분한다.

꼬리표에 의한 정교한 상호작용은 선별, 전문화, 협동을 위한 좋은 토대가된다.

꼬리표에 의한 상호작용은 다시 구성요소들이 계속 변해도 지속되는 메타 행위자와 조직의 창발을 이끈다.

  2. 내부 모형

예측을 위한 도구

    - 묵시적 내부 모형 : 미래의 바람직한 상태에 대한 암묵적인 예견을 통해 단순히 현재의 행위만을 규정함.

    - 명시적 내부 모형 : 대안을 명시적이면서도 내부적으로 찾는 과정을 사용함.

        ex) 미리 가능한 응수를 머릿속으로 그려 보는 것이 대표적임.

모형의 예측을 통해 생명체의 생존 가능성을 높이며 모형은 선택과 적응을 진행해나간다.

  3. 구성단위

어떤 단계에 있는 구성단위를 그 하부 단계의 구성단위의 조합과 상호작용으로 환원할 수 있다.

 * 모든 구성단위의 조합에 대한 규칙을 아는 것은 불가능하다.

필요한 구성단위들을 조합하여 상황을 모형화, 이것을 바탕으로 바람직한 결과를 얻을 수 있는 적절한 대처방법 추출 가능

서로 다른 복잡계의 서로 독립적인 부분을 모아 다른 하나의 복잡계를 만들어 낼 수 있다.

    -> 진화 가능!

 

많은 지적인 생명체가 모여 만들어내는 세계는 정도의 차이는있지만 모두 복잡적응계의 특징을 지닌다! 

4장 : 복잡계 이론을 활용한 은유적 분석

    1. 분석의 틀

여기서의 은유적 분석 : 복잡계 이론을 직관적으로 활용하여 복잡한 세상을 이해하고자 하는 시도

은유적 분석은 분석의 시기와 변화의 주체에 따라 구분하여 접근할 수 있다.

관점 1 : 시스템 내부에 단절적 변화가 발생하기 전에 능동적으로 유도하려는 관점

내부를 인위적으로 변화시키고자 할 때 어떤 프로세스와 전략으로 접근할 것인가?

관점 2 : 시스템 내부에 단절적 변화가 이미 발생한 상황에서 어떻게 변화의 실체를 파악할 것인가의 관점

왜 이러한 현상이 발생했는지 분석하는 관점

관점 3 : 외부환경의 단절적 변화가 발생하기 전에 대응 시스템을 갖추려는 관점

어떻게 외부환경의 단절적 변화에 강건한 시스템 내부를 설계할 것인가?

관점 4 : 이미 외부환경의 단절적 변화가 발생한 상황에서 발빠른 적응을 도모하는 관점

적합도 지형이 바뀐 상황에서 내부 시스템이 어떻게 새로운 지형에 적응할 것인가?

 

관점 1 : 복잡계의 인위적 혁신

시스템이 급격하게 변화하기 위해서는 혼돈의 가장자리에 위치해야 한다.

    -> 시스템의 복잡성을 증대시키는 것과 동일한 말이다.

시스템의 복잡성을 높이기 위해서는...

    1) 열린 시스템 : 시스템이 열려 있으면 외부로부터의 에너지 유입이 가능하다.

외부와 단절되어 정보를 받아들이지 못하면, 시스템 내부의 구성원들은 획일화될 것이다.

외부와의 지속적인 정보 교환 -> 내부의 구성원들은 다양한 방식으로 적응 -> 복잡성 증가!

    2) 시스템의 구성요소를 작게 쪼개고 구성요소의 대칭성 파괴

구성요소 분해 -> 각 요소가 차별화될 가능성 상승, 각 요소마다 환경의 섭동에 다르게 대응할 가능성이 높음

 + 구성요소간 대칭성 파괴 -> 구성요소가 다양해지고 복잡성도 증가.

    3) 구성요소의 상호작용 증대

쪼갠 구성요소의 상호작용을 징대시킬수록 복잡성 증대

복잡한 상호작용은 다양한 되먹임을 통한 새로운 질서의 형성 가능

    4) 전체 시스템과 구성요소의 공진화

세스템을 상위 시스템(supersystem : 메타 행위자), 하위 시스템(subsystem : 행위자)으로 구분했을 때 두 시스템은 공진화 해야 한다는 의미

    5) 행위자의 무작위한 일탈을 제어하기 위한 적절한 규칙

행위자들의 제어규칙이 있을 때... -> 시스템 불확정성 감소 -> 복잡성 상승

제어규칙 : 행위자 개개인 상호작용에 대한 가이드라인 (획일화 x!!!)

일어난 변화를 성공적으로 정착시키려면..

    1) 변화를 고착화(Lock-in)  -> ex) 표준화, 교체비용(switching cost) 높이기, 특허, 진입장벽 높이기

    2) 시스템에 지속적으로 에너지 주입

고착화되지 않았다면, 시스템은 다시 제자리로 회귀하려는 성질을 가진다.

ex) 새로운 질서가 구성원들에게 체질화될 때까지 지속적인 관심을 가지고 모니터링

 

관점 2 : 단절적 변화의 실체 파악

시스템에 이미 단절적 변화가 생겼다면 왜 이러한 현상이 발생했는지에 대해 실체를 파악하는 것이 중요

창발현상의 원인을 밝히기 위한 5단계 프로세스

    1) 시스템이 복잡적응계인가?

시스템의 구성요소는?   구성요소들이 상호작용을 하는가?   열린 시스템인가?   열린시스템이면 어떤 에너지나 자원이 출입하고 있는가?

    2) 시스템이 혼돈의 가장자리에 위치했는가?

급진적 변화의 소용돌이 이전의 평형상태의 시스템에 어떤 변화가 있었는가?

복잡성이 증가했는가? 증가했다면 실제로 어떤 일들이 발생했는가?

    3) 섭동이나 요동이 있었는가?

임계점이 어디이며, 임계점을 통과할 때 어떤 일들이 있었는가?

    4) 자기조직화 현상이 있었는가?

양의 되먹임 고리가 만들어졌는가?    프랙탈이 만들어지고 공진화했는가?

시스템이 임계점을 통과한 후 어떤 과정으로 폭발적인 변화를 하게 되었는가?

    5) 복잡하지만 안정적인 새로운 시스템이 만들어졌는가?

시스템이 고착되었는가?   시스템에 지속적으로 에너지가 유입되는가?

최종적으로 변화된 시스템이 새로운 질서를 형성했는지 분석한다. 매우 안정적인 소산구조를 형성했는지를 분석해야 한다는 의미이다.

 

관점 3 : 외부의 변화에 강건한 시스템 설계

시스템 외부환경에 단절적 변화가 발생했을 때 시스템의 항상성을 유지하기 위해 어떻게 해야 할 것인가에 대한 이슈

'관점 1'에서 언급한 복잡성을 증가시키는 다섯 가지 방법과 전채적으로 맥을 같이한다.

복잡성을 증대시킨다는 것은 동전의 양면과 같아서 외부의 섭동으로부터 시스템의 항상성을 유지시키도 하지만, 시스템 내부를 혼돈의 가장자리로 몰아서 창발을 유도하는 역할도 하는 것이다.

 

관점 4 : 외부의 변화에 신속 적응

시스템 외부에서 단절적 변화가 발생했을 때 시스템이 어덯게 적응할 것인가?

외부의 단절적 변화가 발생한 것은 적합도 지형 자체가 바뀐 상황이다!

    1) 바뀐 지형에서 가장 가까운 봉우리로 올라가기 위해 기존의 종들과 치열한 싸움 or 협력

진화론 : 환경이 변화했을 때 그에 대한 적응방법으로 교배를 통한 교차와 유사함.

경쟁에서 승리하기 위한 방법의 하나로 '협력'을 생각할 수 있다.

    2) 경쟁이 치욜하지 않을 것 같은 봉우리로 옮겨가는 변신

진화론 : 우연적 요인에 의해 돌연변이가 발생한 상황

    3) 적합도 지형 자체를 변화시키기

경쟁으로 인한 위험도는 감소하지만, 새로운 봉우리를 만드는 과정이 쉽지 않다.

 

4장은 이 이후에 은유적 분석을 '사례1~4'를 통해서 세부적으로 보여준다. 이 부분이 궁금하다면 직접 읽어보자.

꽤 괜찮다.

 

5장 : 복잡계 연구의 방법론

    1. 행위자 기반 모형(Agent-Based Modeling)

'행위자' 수준에 초점을 맞춘 모형이다.

행위자, 행위자가 활동하고 상호작용 하는 시스템 공간, 시스템에 영향을 끼치는 외부환경 등의 세 가지 요소로 구성되고, 각각에 어떠한 규칙을 부여해서 만드는 모형이다.

손으로 못한다. 컴퓨터로 코딩 해야 된다.

        1) 행위자가 갖춰야 할 네 가지 요소

행위자는 내부 데이터(행위자 자신의 상태), 내부 데이터 수정 방법(주변상황을 어떻게 받아들일까?), 행동 규칙(행위자가 어떻게 행동하고 의사결정 할 것인가?), 행동규칙을 수정하는 방법(자신의 상황이 바뀌었을 때 어떻게 행동규칙을 바꿀 것인가?) 를 고려해야 한다.

        2) 시스템 공간

물리적인 공간일 필요는 없다. 왼쪽 그림처럼 추상적이더라도 코딩으로 구현할 수 있으면 상관 없다.

사각 격자형 시스템 공간, 육각 격자형 시스템 공간, 토러스형 공간 등 자기 입맛대로 사용하면 된다.

뿐만 아니라, 지리정보 시스템(GIS: Geographic Information System)의 정보를 이용하는 방법도 있으며, 네트워크형으로 공간을 만드는 방법도 있다.

 

        3) 외부환경

적절한 확률변수로 나타내거나, 과거 데이터에서 얻어낸 단순한 주기함수로 외부환경을 나타낸다.

이를 '행위자 일부에게 국소적으로 적용'하는 경우와 '시스템 전체에 전역적으로 적용'하는 경우도 고려해야 할 것이다.

 

행위자 기반 모형의 특징

1) 행위자의 내부구조 측면

  - 내부 자유도(internal degrees of freedom) : 행위자의 특성이 적절한 내부 변수로 나타내져야 한다.

    ex) 밖에 많이 돌아다니는 사람과 주로 집에 있는 사람을 변수로 표현해야 한다.

  - 자율성(autonomy) : 자신의 내부상태와 외부환경을 인지하여 행위자가 자율적으로 행동

2) 행위자의 행동 측면

  - 국소성(locality) : 당연하겠지만, 개별 행위자의 행동이 전체 시스템을 즉각적으로 변화시키지 않는다는 것을 말함.

  - 이동성(mobility) : 행위자는 공간을 따라 이동할 수 있음.

  - 반응성(reactivity) : 행위자는 환경을 감지하고 거기에 대응한다. 다른 행위자나 환경변화에 의해 유도될 수 있지만, 대응 방식은 자율적으로 정한다.

  - 선행성(proactivity) : 행위자는 환경변화를 선도하기도 한다.(애플의 iPhone 같은거...)

3) 행위자의 다중성과 전체 시스템 측면

  - 모듈성(modularity) : 공통적인 특징을 모듈화

  - 기능성(functionality) : 시스템 전체적인 특징과 행위자의 특성은 일치하지 않는다. 따라서 행위자의 특성을 설정할 때 주의하자.

  - 적응성(adaptivity) : 행위자는 주변 행위자와 환경변화에 따라 스스로의 변화를 모색할 수 있다.

    -> 새로운 판단규칙과 반응규칙을 담을 수 있는 능력은 보통 제한되어 있음을 명심하자.(보통 기억에 한계를 둔다.)

 

사실, 행위자 기반 모형을 조금이라도 들어봤다면 당연하다고 생각 할 수 있을 것이다.

그리고, 행위자의 지능 수준에 따라서 나뉘기도 한다. 이는 자기가 만들 모형에 맞게 직접 조절하면 된다.

딱히 의미가 있지 않다.

    2. 복잡 네트워크

 

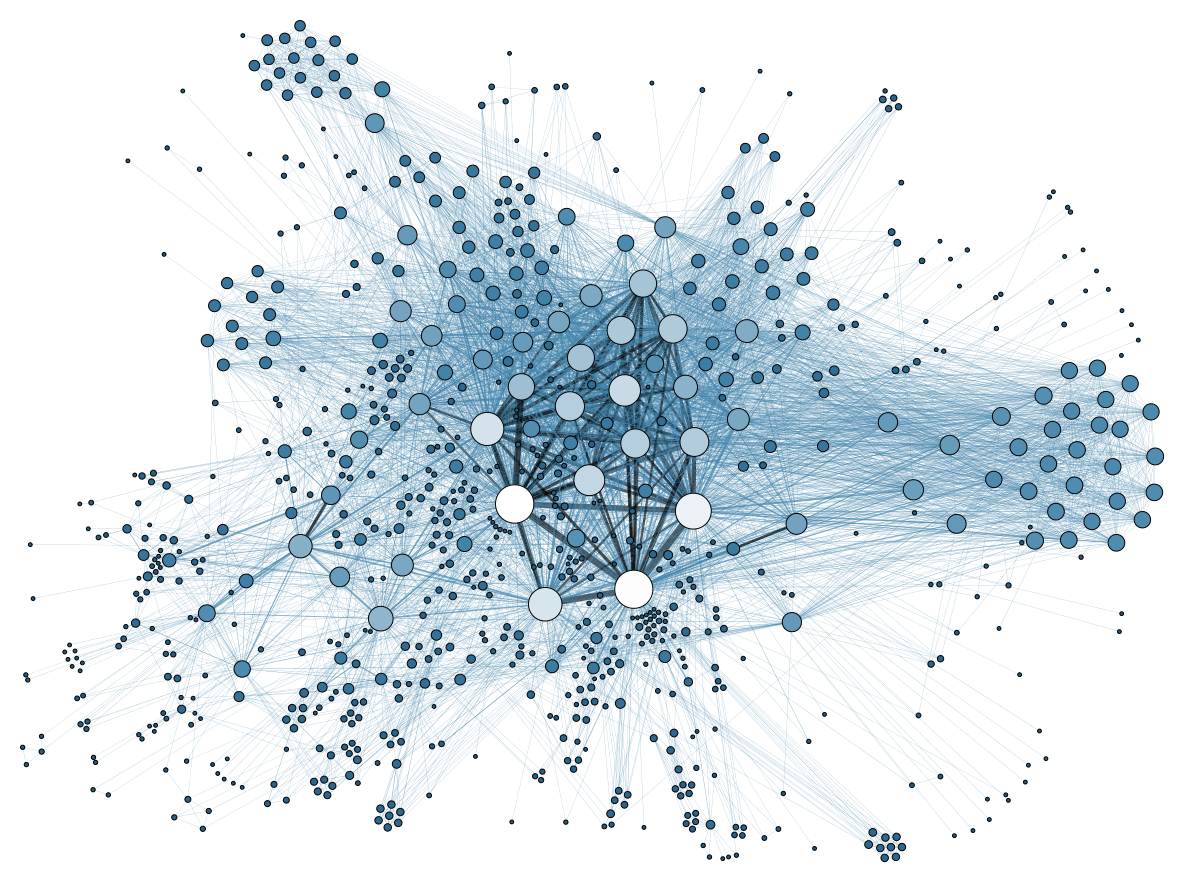
복잡 네트워크. 그냥 왼쪽 그림으로 설명이 끝난다.

점은 '노드'라고 부르고, 선은 '링크'라고 부른다.

-끝-

은 아니지만, 진짜 딱히 없다.

 

연결성(connectivity)의 문제를 주로 다룬다.

모든 링크가 대등하다고 하느 경우도 있지만 가중치(weight)가 있는 경우도 있다.

  ex) 거래규모가 큰 것에 높은 가중치...!

이거를 어떻게 분석할까.

연결수(degree) 분포 : 각 노드에 붙어 있는 링크의 개수를 degree라고 한다. 그러면 각 노드의 연결수가 어떤 분포를 가질까?

위쪽 그림에서 보면 중앙에 매우 많은 연결관계를 맺고 있는 노드들이 있다. 이를 '허브(hub)'라고 부른다.

이웃 노드의 평균 연결수(average nearest-neighbor degree)

삼각관계, 결속계수 등으로 네트워크를 분석한다.

 

네트워크에도 정규 네트워크, 좁은 세상 네트워크, 무작위 네트워크 등의 종류가 있다.

    3. 시스템 다이내믹스

접근방법의 특징

  1) 연구하고자 하는 특정 변수가 시간의 변화에 따라 어떻게 동태적으로 변화해가는가?

  2) 모든 현상을 시스템 변수의 원형의 되먹임 관점에서 이해한다.

  3) 사실적 사고(operational thinking)에 초점을 맞춘다.  -> 실제로 어떻게 일어나는지 변화의 과정에 초점

직접 모델을 만드는 등 어려워 해서 시스템 사고(system thinking)이라는 여역이 분리됨.

    -> 시스템의 작동 메커니즘을 직관적으로 파악하여 시스템을 효과적으로 변화시킬 수 있느 ㄴ전략을 발견하기 위한 사고방식.

 

시스템 사고의 절차

아래의 방법으로 시스템을 이해하는걸로 끝내는 것이 아니라, 원하는 방향으로 시스템을 변화시킬 수 있는 전략을 찾는 것이 중요하다.

  1) 시스템의 지속적인 변화를 인정하는 파동의 사고(Wave Thinking)

    파동의 전파성, 간섭성, 공명성 등을 명심하자.

  2) 인과관계를 바라보는 인과적 사고(Causal Thinking)

다음과 같은 원칙을 지키자.

    (1) : 원인과 결과의 부호는 항상 변화할 수 있다.

    (2) : 하나의 시스템에서는 단 하나의 인과관계만 허용된다.

    (3) : 여러 가지 인과관계가 존재한다고 여겨지는 경우 제 3의 변수가 매개하고 있는지 고려하자.

  3) 인과관계의 사슬이 순환되는 구조를 강조하는 되먹임 사고(Feedback Thinking)

시스템 사고의 핵심이다.

되먹임이 존재하기 때문에 시스템이 비선형성을 가지며 변화한다.

  4) 전략적 지렛대(Strategic Leverage)

시스템 사고의 궁극적인 목적은 시스템을 변화시킬 수 있는 전략을 발견하는 데 있다.

작은 힘으로 큰 변화를 가져올 수 있는 전략을 찾는다. 이를 넓은 의미에서 전략적 지렛대라고 한다.

변수를 직접 공략하는 것 보다, 변수를 움직이는 메커니즘을 이해하는 것이 중요하다.

    (1) 되먹임 구조에서 객체와 주체를 이해하자.

    (2) 되먹임 구조 내에서 공격할 지점을 결정하고 언제 공격할 것인지 결정하자. -> 시뮬레이션 필수

    (3) 새로운 되먹임 구조의 생성 및 기존 되먹임 구조의 변경을 통해 계 자체를 새롭게 설계하자.

 

system thinking. 그냥 이거다.

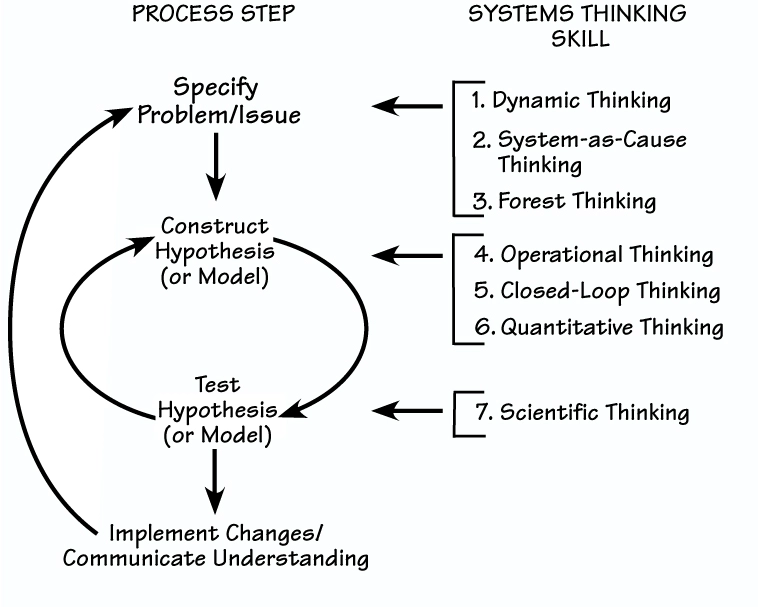
위 사진을 누르면 나오는 글이 있는데 한번 읽어보자.

예시)

예시.

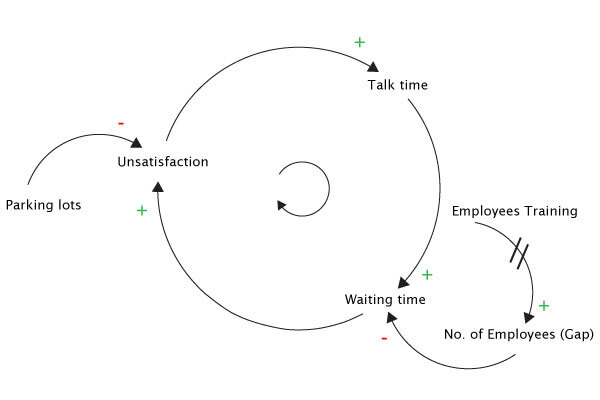
위 사진을 누르면 나오는 페이지에도 잘 설명되어 있다.(물론 영어다.)

한글로 된 예시.

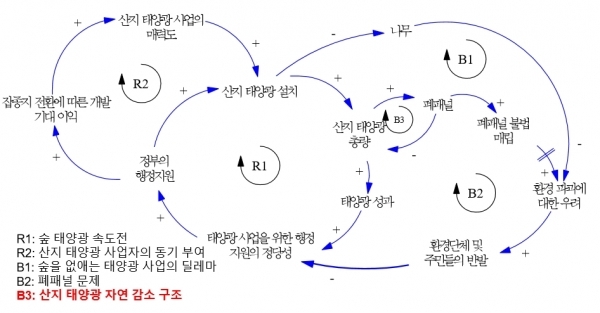
    4. 비선형시계열 분석

시계열(time series) : 일정 시간 간격으로 배치된 데이터들.

ex) KOSPI 일별 종가

데이터만 보면 어떤 일이 일어나고 있는지 알 수 없다. 측정한 시계열의 특징을 잡아내어 거의 똑같은 시계열을 만드는 것을 목표로 한다.

 

비선형시계열 분석 절차

1. 시계열 안정성(stationarity) 확인

  1-1) 강한 안정성(strong form of stationarity)

어떤 시간에 시계열 표본을 측정하더라도 확률분포가 일정할 경우.

  1-2) 약한 안정성(weak form of stationarity)

어떤 시간에 시계열 표본을 측정하더라도 평균과 분산, 공분산(1차 및 2차 모멘트)이 일정할 경우.

 * 실질적인 연구에서는 다른 안정성의 척도를 고려한다.

    -> 자기상관(autocorrelation), 파워 스펙트럼(power spectrum) 분석 등

 

2. 선형시계열 모형의 적용

ARMA(autoregressive moving average)모형

FRM에서 배운게 여기서 나와서 반갑다.(물론, 훈련소에서 읽을때는 몰랐고, 다시 독후감 쓰려고 대충 훑을때 이다.)

AR : $X_t = c+\Sigma \phi_i X_{t-i} + \epsilon_t$ -> 과거의 값 + 적당한 잡음

MA : $X_t = \Sigma \theta_i epsilon_{t-i} + \epsilon_t$ -> 이전의 잡음 + 이번 잡음

 

3. 선형시계열 모형의 유효성 검증

머신러닝과 딥러닝을 대충이라도 배워본 사람이라면 알 것이다.

단순하게, 전체 데이터의 일부분을 'test set'으로 두고, 나머지 가지고 모델을 학습시킨다.

그 후, test set에 적용시켜서 제대로 설명하는지 확인하는 것이다.

 

4. 시계열의 혼돈성 확인

  4-1) 시간지연좌표의 구성

시계열 ${a_t} = {a_t, a_{t-1}, a_{t-2}, ......}$이거를 다음과 같이 '시간자연좌표($d_t$)'를 그리면...

${d_t} = {(a_t, a_{t-\tau}, a_{t-2\tau})}$ 이렇게 바뀐다. 이렇게 하고 그래프를 그려도 정규분포처럼 잘 나오면

    -> 시계열이 혼돈적이구나!

  4-2) 리아푸노프 지수($\lambda$)의 계산

혼돈의 특성대로 초기조건의 작은 차이가 시간이 지나면서 얼마나 크게 변화하는지를 나타낸 값.

시간에 비례해서 벌어지는것이 아니라, 지수함수적으로 급격히 멀어지는 것 -> 이때 지수값이 리아푸노프 지수

점 끌개로 수렴 -> $\lambda < 0$

한계순환 및 토러스 끌개로 수렴 -> $\lambda = 0$

기이한 끌개로 수렴 -> $0 < \lambda < \infty$

잡음(무작위) -> $\lambda \rightarrow \infty$

 

  4-3) 상관차원(Correlation dimension)의 계산

5. 원시 데이터와 대리 데이터 분석 비교

* 결정론적이 아니라 확률론적인 과정에서 만들어진 모조 데이터를 이용해 검증해보는 단계.

6. 혼돈계 모형의 적용

7. 혼돈계 모형의 유효성 검증

8. 혼돈계 모형을 이용한 예측

 

이 이후는 예시들이다. 너무 길어지기도 하고, 너무 힘들어서...(이거 안끝내면 책 읽을 맛이 안난다...)

여기서 끝!

 

물론, 재미있는 책이었다. 재미있는 책인데... 이걸 '다시' 읽고 독후감을 남긴다는게 너무 고통스럽다. ;;

 

<출처>

반응형
저작자표시 비영리 변경금지

'독후감' 카테고리의 다른 글

현명한 투자자  (2) 2024.12.19
넛지(파이널 에디션)  (1) 2024.12.05
레이 달리오의 금융 위기 템플릿  (1) 2023.11.15
부를 재편하는 금융 대혁명  (0) 2023.02.19
노이즈 : 생각의 잡음  (0) 2023.01.18

'독후감'의 다른글

  • 현재글복잡계 개론

관련글

티스토리툴바